本文我们将研究一些在反向传播发展之后取得快速进展的研究，直到90年代后期，我们将在后面看到它们是深度学习的基本基础。

第二部分：神经网络的苏醒

基于神经网络的计算机视觉

随着训练多层神经网络的谜题被揭开，这个话题再一次变得空前热门，罗森布拉特的崇高雄心似乎也将得以实现。直到1989年另一个关键发现被公布，现在仍广为教科书及各大讲座引用出版¹：“多层前馈网络是通用逼近器”。从本质上讲并在数学上得以证明：多层可让神经网络在理论上能实现各种功能，当然也包括抑或逻辑（XOR）。

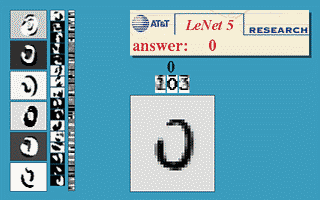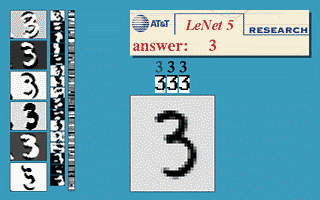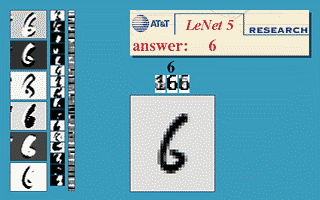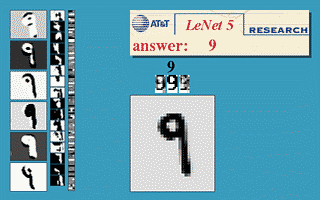
然而，这是数学，你可以在数学中畅想自己拥有无限内存和所需计算能力——反向传播可以让神经网络被用于世界任何角落吗？噢，当然。也是在1989年，Yann LeCunn在AT&T Bell实验室验证了一个反向传播在现实世界中的杰出应用，即「反向传播应用于手写邮编识别（Backpropagation Applied to Handwritten Zip Code Recognition）」²。

你或许会认为，让计算机能够正确理解手写数字并没有那么了不起，而且今天看来，这还会显得你太过大惊小怪，但事实上，在这个应用公开发布之前，人类书写混乱，笔画也不连贯，对计算机整齐划一的思维方式构成了巨大挑战。这篇研究使用了美国邮政的大量数据资料，结果证明神经网络完全能够胜任识别任务。更重要的是，这份研究首次强调了超越普通（plain）反向传播 、迈向现代深度学习这一关键转变的实践需求。

传统的视觉模式识别工作已经证明，抽取局部特征并且将它们结合起来组成更高级的特征是有优势的。通过迫使隐藏单元结合局部信息来源，很容易将这样的知识搭建成网络。一个事物的本质特征可以出现在输入图片的不同位置。因此，拥有一套特征探测器，可以探测到位于输入环节任何地方的某个具体特征实例，非常明智。既然一个特征的精准定位于分类无关，那么，我们可以在处理过程中适当舍弃一些位置信息。不过，近似的位置信息必须被保留，从而允许下面网络层能够探测到更加高级更加复杂的特征。（Fukushima1980，Mozer,1987）

或者，更具体的：神经网络的第一个隐层是卷积层——不同于传统网络层，每个神经元对应的一个图片像素都相应有一个不同的权值（40 * 60 = 2400 个权值），神经元只有很少一部分权值（5 * 5 = 25）以同样的大小应用于图像的一小个完整子空间。所以，比如替换了用四种不同的神经元来学习整个输入图片4个角的45度对角线探测，一个单独的神经元能通过在图片的子空间上学习探测45度对角线，并且照着这样的方法对整张图片进行学习。每层的第一道程序都以相类似的方式进行，但是，接收的是在前一隐藏层找到的「局部」特征位置而不是图片像素值，而且，既然它们正在结合有关日益增大的图片子集的信息，那么，它们也能「看到」其余更大的图片部分。最后，倒数的两个网络层利用了前面卷积抽象出来的更加高级更加明显的特征来判断输入的图像究竟该归类到哪里。这个在1989年的论文里提出的方法继续成为举国采用的支票读取系统的基础，正如LeCun在如下小视频中演示的：

1993 年卷积网络识别手写数字示例

这很管用，为什么？原因很直观，如果数学表述上不是那么清楚的话：没有这些约束条件，网络就必须学习同样的简单事情（比如，检测45°角的直线和小圆圈等），要花大把时间学习图像的每一部分。但是，有些约束条件，每一个简单特征只需要一个神经元来学习——而且，由于整体权值大量减少，整个过程完成起来更快。此外，既然这些特征的像素确切位置无关紧要，在计算应用权重时，基本上可以跳过图像相邻子集——子采样，现在称为共享池手段（a type of pooling）——当应用权值时，进一步减少了训练时间。多加的这两层（卷积层和共享池层）——是卷积神经网络（CNNs/ConvNets）和普通旧神经网络的主要区别。

卷积神经网络（CNN）的操作过程

那时，卷积的思想被称作「权值共享」，也在1986年Rumelhart、Hinton和Williams³关于反向传播的延伸分析中得到了切实讨论。实际上，卷积思想又回到更早之前了——Minsky和Papert在1969年《感知机》中的分析完全可以提出激发这一研究想法的问题。但是，和之前一样，其他人已经独立地对其进行了研究——比如，Kunihiko Fukushima在1980年提出的 Neurocognitron⁴。而且，和之前一样，这一思想从大脑研究汲取了灵感：

“根据Hubel和Wiesel的层级模型，视觉皮层中的神经网络具有一个层级结构：LGB（外侧膝状体）→样品细胞→复杂细胞→低阶超复杂细胞->高阶超复杂细胞。低阶超复杂细胞和高阶超复杂细胞之间的神经网络具有一个和简单细胞与复杂细胞之间的网络类似的结构。在这种层状结构中，较高级别的细胞通常会有这样的倾向，即对刺激模式的更复杂的特征进行选择性响应，同时也具有一个更大的接收域，而且对刺激模式位置的移动更不敏感。因此，在我们的模型中就引入了类似于层级模型的结构。”

LeCun也在贝尔实验室继续支持卷积神经网络，其相应的研究成果也最终在上世纪90年代中期成功应用于支票读取——他的谈话和采访通常都介绍了这一事实：「在上世纪90年代后期，这些系统当中的一个读取了全美大约10%到20%的支票。」⁵

神经网络进入无监督期

将死记硬背，完全无趣的支票读取工作自动化，就是机器学习大展拳脚的例子。也许有一个预测性小的应用？ 压缩。即指找到一种更小体量的数据表示模式，并从其可以恢复数据原有的表示形态，通过机器学习找到的压缩方法有可能会超越所有现有的压缩模式。当然，意思是在一些数据中找到一个更小的数据表征，原始数据可以从中加以重构。学会压缩这一方案远胜于常规压缩算法，在这种情况下，学习算法可以找到在常规压缩算法下可能错失的数据特征。而且，这也很容易做到——仅用训练带有一个小隐藏层的神经网络就可以对输入进行输出:

一个自编码神经网络

自编码神经网络

这是一个自编码神经网络，也是一种学习压缩的方法——有效地将数据转换为压缩格式，并且自动返回到本身。我们可以看到，输出层会计算其输出结果。由于隐藏层的输出比输入层少，因此，隐藏层的输出是输入数据的一个压缩表达，可以在输出层进行重建。

更明确地了解自编码压缩

注意一件奇妙的事情：我们训练所需的唯一东西就是一些输入数据。这与监督式机器学习的要求形成鲜明的对比，监督式机器学习需要的训练集是输入-输出对（标记数据），来近似地生成能从这些输入得到对应输出的函数。确实，自编码器并不是一种监督式学习；它们实际上是一种非监督式学习，只需要一组输入数据（未标记的数据），目的是找到这些数据中某些隐藏的结构。换句话说，非监督式学习对函数的近似程度不如它从输入数据中生成另一个有用的表征那么多。这样一来，这个表征比原始数据能重构的表征更小，但它也能被用来寻找相似的数据组（聚类）或者潜在变量（latent variables）的其他推论（某些从数据看来已知存在但数值未知的方面）。

聚类，一种很常用的非监督式学习应用

在反向传播算法发现之前和之后，神经网络都还有其他的非监督式应用，最著名的是自组织映射神经网络（SOM，Self Organizing Maps）⁶和自适应共振理论（ART，Adapative Resonance Theory）⁷。SOM能生成低维度的数据表征，便于可视化，而ART能够在不被告知正确分类的情况下，学习对任意输入数据进行分类。如果你想一想就会发现，从未标记数据中能学到很多东西是符合直觉的。假设你有一个数据集，其中有一堆手写数字的数据集，并没有标记每张图片对应着哪个数字。那么，如果一张图片上有数据集中的某个数字，那它看起来与其他大多数拥有同样数字的图片很相似，所以，尽管计算机可能并不知道这些图片对应着哪个数字，但它应该能够发现它们都对应着同一个数字。这样，模式识别就是大多数机器学习要解决的任务，也有可能是人脑强大能力的基础。但是，让我们不要偏离我们的深度学习之旅，回到自编码器上。

自组织映射神经网络：将输入的一个大向量映射到一个神经输出的网格中，在其中，每个输出都是一个聚类。相邻的神经元表示同样的聚类。

正如权重共享一样，关于自编码器最早的讨论是在前面提到过的1986年的反向传播分析中所进行。有了权重共享，它在接下来几年中的更多研究中重新浮出了水面^{8 9}，包括Hinton自己¹⁰。这篇论文，有一个有趣的标题：《自编码器，最小描述长度和亥姆霍兹自由能》（Autoencoders, Minimum Description Length, and Helmholts Free Energy），提出「最自然的非监督式学习方法就是使用一个定义概率分布而不是可观测向量的模型」，并使用一个神经网络来学习这种模型。所以，还有一件你能用神经网络来做的奇妙事：对概率分布进行近似。

神经网络迎来信念网络

事实上，在成为1986年讨论反向传播学习算法这篇有重大影响力论文的合作者之前，Hinton在研究一种神经网络方法，可以学习1985年《A Learning Algorithm for Boltzmann Machines》¹¹中的概率分布。玻尔兹曼机就是类似神经网络的网络，并有着和感知器（Perceptrons）非常相似的单元，但该机器并不是根据输入和权重来计算输出，在给定相连单元值和权重的情况下，网络中的每个单元都能计算出自身概率，取得值为1或0。因此，这些单元都是随机的——它们依循的是概率分布而非一种已知的决定性方式。玻尔兹曼部分和概率分布有关，它需要考虑系统中粒子的状态，这些状态本身基于粒子的能量和系统本身的热力学温度。这一分布不仅决定了玻尔兹曼机器数学方法，也决定了其推理方法——网络中的单元本身拥有能量和状况，学习是由最小化系统能量和热力学直接刺激完成的。虽然不太直观，但这种基于能量的推理演绎实际上恰是一种基于能量的模型的例子，并能够适用于基于能量的学习理论框架，而很多学习算法都能用这样的框架进行表述。¹²

附：基于能量模型的更多内容

对于一堆学习方法而言，有一个共同的理论框架并不令人意外，归根到底，所有的学习都归结为优化，引用上面引用内容：

“训练一个 EBM 包括找到一个能产生最好的 Y 和 任何 X 的能量函数…… EBM 的架构师参数化能量函数 E(W, Y, X) 的内部结构……这种质量检测称为损失函数（即函数的函数）并表示为 L(E, S)。…… 为找到最好的能量函数[]，我们需要一种方法来评估任何特定的能量函数的质量，完全基于两个要素：训练集和我们对任务的先前知识。简单起见，我们经常用 L(W, S)来表示它，并简单称之为损失函数。学习问题很简单，就是找到最小化损失的 W。”

因此基于能量的模型的关键是认识到所有这些算法从本质上讲是用不同的方法来优化这一对函数：能量函数 E 和损失函数 L，通过找到一组好的值到一堆变量，表示为 W，输入的数据为 X，输出为 Y。这对于一个框架来说确实是一个非常广泛的定义，但是仍然很好地封装了很多算法从根本上再做的事。

一个简单的信念网络/贝叶斯网络

一个简单的信念，或者说贝叶斯网络——玻尔兹曼机器基本上就是如此，但有着非直接/对称联系和可训练式权重，能够学习特定模式下的概率。

回到玻尔兹曼机器。当这样的单元一起置于网络中，就形成了一张图表，而数据图形模型也是如此。本质上，它们能够做到一些非常类似普通神经网络的事：某些隐藏单元在给定某些代表可见变量的可见单元的已知值（输入——图像像素，文本字符等）后，计算某些隐藏变量的概率（输出——数据分类或数据特征）。以给数字图像分类为例，隐藏变量就是实际的数字值，可见变量是图像的像素；给定数字图像「1」作为输入，可见单元的值就可知，隐藏单元给图像代表「1」的概率进行建模，而这应该会有较高的输出概率。

玻尔兹曼机器实例

玻尔兹曼机器实例。每一行都有相关的权重，就像神经网络一样。注意，这里没有分层——所有事都可能跟所有事相关联。我们会在后文讨论这样一种变异的神经网络

因此，对于分类任务，现在有一种计算每种类别概率的好方法了。这非常类似正常分类神经网络实际计算输出的过程，但这些网络有另一个小花招：它们能够生成看似合理的输入数据。这是从相关的概率等式中得来的——网络不只是会学习计算已知可见变量值时的隐藏变量值概率，还能够由已知隐藏变量值反推可见变量值概率。所以，如果我们想得出一幅「1」数字图像，这些跟像素变量相关的单元就知道需要输出概率1，而图像就能够根据概率得出——这些网络就是生成图像模型。虽然可能能够实现目标非常类似普通神经网络的监督式学习，但学习一个好的生成模型的非监督式学习任务——概率性地学习某些数据的隐藏结构——是这些网络普遍所需要的。这些大部分都不是小说，学习算法确实存在，而使其成为可能的特殊公式，正如其论文本身所描述的：

“或许，玻尔兹曼机器公式最有趣的方面在于它能够引导出一种（与领域无关的）一般性学习算法，这种算法会以整个网络发展出的一种内部模型（这个模型能够捕获其周围环境的基础结构）的方式修改单元之间的联系强度。在寻找这样一个算法的路上，有一段长时间失败的历史（Newell，1982），而很多人（特别是人工智能领域的人）现在相信不存在这样的算法。”

附：玻尔兹曼机的更多解释

我先学习了经典神经网络模型，花了一些时间来理解这些概率网络的概念。为了说明，我引用一下论文里的内容：

“网络修改其连接的强度，从而构建一个内部生成模型，生成与实例相同概率分布的实例。然后，当显示任何特定的实例时，网络可以通过在内部模型中找到将生成该实例的变量的值来‘解释’它。

…

该机由被称为单元的原始计算单元组成，这些单元通过双向链路相互连接。一个单元总是处于两种状态之一，即开或关，它将这些状态作为其相邻单元状态的概率函数，以及与其相连接的权重。权重可以取任何符号的实际值。开启或关闭的单元意味着系统目前接受或拒绝关于域的一些基本假设。链路上的权重表示两个假设之间的弱成对约束。正数的权重表明这两个假设倾向于相互支持；如果当前假定被接受，则另一个更有可能被接受。相反的，负数权重表明，和正数权重其他方面一样，但却是两个假设不能被全部接受。链路权重是对称的，在两个方向上具有相同的强度（Hinton & Sejnowski, 1983）。”

我们就不展开算法的全部细节了，就列出一些亮点：这是最大似然算法的变体，这简单意味着它追求与已知正确值匹配的网络可见单元值（visible unit values）概率的最大化。同时计算每个单元的实际最有可能值 ，计算要求太高，因此，训练吉布斯采样（training Gibbs Sampling）——以随机的单元值网络作为开始，在给定单元连接值的情况下，不断迭代重新给单元赋值——被用来给出一些实际已知值。当使用训练集学习时，设置可见单位值（ visible units）从而能够得到当前训练样本的值，这样就通过抽样得到了隐藏单位值。一旦抽取到了一些真实值，我们就可以采取类似反向传播的办法——针对每个权重值求偏导数，然后估算出如何调整权重来增加整个网络做出正确预测的概率。

和神经网络一样，算法既可以在监督（知道隐藏单元值）也可以在无监督方式下完成。尽管这一算法被证明有效（尤其是在面对自编码神经网络解决的「编码」问题时），但很快就看出不是特别有效。Redford M. Neal 1992年的论文《Connectionist learning of belief networks》¹³论证了需要一种更快的方法，他说：「这些能力使得玻耳兹曼机在许多应用中都非常有吸引力——要不是学习过程通常被认为是慢的要命。」因此，Neal引入了类似信念网络的想法，本质上就像玻耳兹曼机控制、发送连接（所以又有了层次，就像我们之前看过的神经网络一样，而不像上面的玻耳兹曼机控制机概念）。跳出了讨厌的概率数学，这一变化使得网络能以一种更快的学习算法得到训练。洒水器和雨水那一层上面可以视为有一个信念网络——这一术语非常严谨，因为这种基于概率的模型，除了和机器学习领域有着联系，和数学中的概率领域也有着密切的关联。

信念网络的解释

尽管这种方法比玻尔兹曼机进步，但还是太慢了，正确计算变量间的概率关系的数学需求计算量太大了，而且还没啥简化技巧。Hinton、Neal和其他两位合作者很快在1995年的论文《The wake-sleep algorithm for unsupervised neural networks》¹⁴唤醒算法中提出了一些新技巧。这次他们又搞出一个和上个信念网络有些不一样的网络，现在被叫做「亥姆霍兹机」¹⁵。再次抛开细节不谈，核心的想法就是对隐含变量的估算和对已知变量的逆转生成计算采取两套不同的权重，前者叫做recognition weights，后者叫做generative weights，保留了Neal’s信念网络的有方向的特性。这样一来，当用于玻尔兹曼机的那些监督和无监督学习问题时，训练就快得多。

附：唤醒算法的简化假设

在 Hinton 谈论唤醒算法的视频中，他经常提醒简化假设的严重程度，结果证明算法不管用。我将再次引用论文本身来解释这个假设：

“The key simplifying assumption is that the recognition distribution for a particular example d, Q is factorial (separable) in each layer. If there are h stochastic binary units in a layer B, the portion of the distribution P(B,d) due to that layer is determined by 2^(h - 1) probabilities. However, Q makes the assumption that the actual activity of any one unit in layer P is independent of the activities of all the other units in that layer, given the activities of all the units in the lower layer, l - 1, so the recognition model needs only specify h probabilities rather than 2” - 1. The independence assumption allows F(d; 8.4) to be evaluated efficiently, but this computational tractability is bought at a price, since the true posterior is unlikely to be factorial

…

The generative model is taken to be factorial in the same way, although one should note that factorial generative models rarely have recognition distributions that are themselves exactly factorial.”

注意 Neal 的信念网络也隐含地使得概率因子分解成只有前向定向连接的单元层。

最终，信念网络的训练多少会快些！尽管没那么大的影响力，对信念网络的无监督学习而言，这一算法改进是非常重要的进步，堪比十年前反向传播的突破。不过，目前为止，新的机器学习方法也开始涌现，人们也又开始质疑神经网络，因为大部分的想法似乎基于直觉，而且因为计算机仍旧很难满足它们的计算需求，人工智能寒冬将在几年内到来。

本部分结束。

参考：

http://www.andreykurenkov.com/writing/a-brief-history-of-neural-nets-and-deep-learning-part-2/ https://mp.weixin.qq.com/s/iXtyLK8YHxQT09JufNF4EA##