游戏智能的诞生
本节介绍 AI 的诞生及在数字计算机上运行的首个 AI 游戏。
故事开始,人类是如何使电脑擅长下围棋的 | 2016-04-18
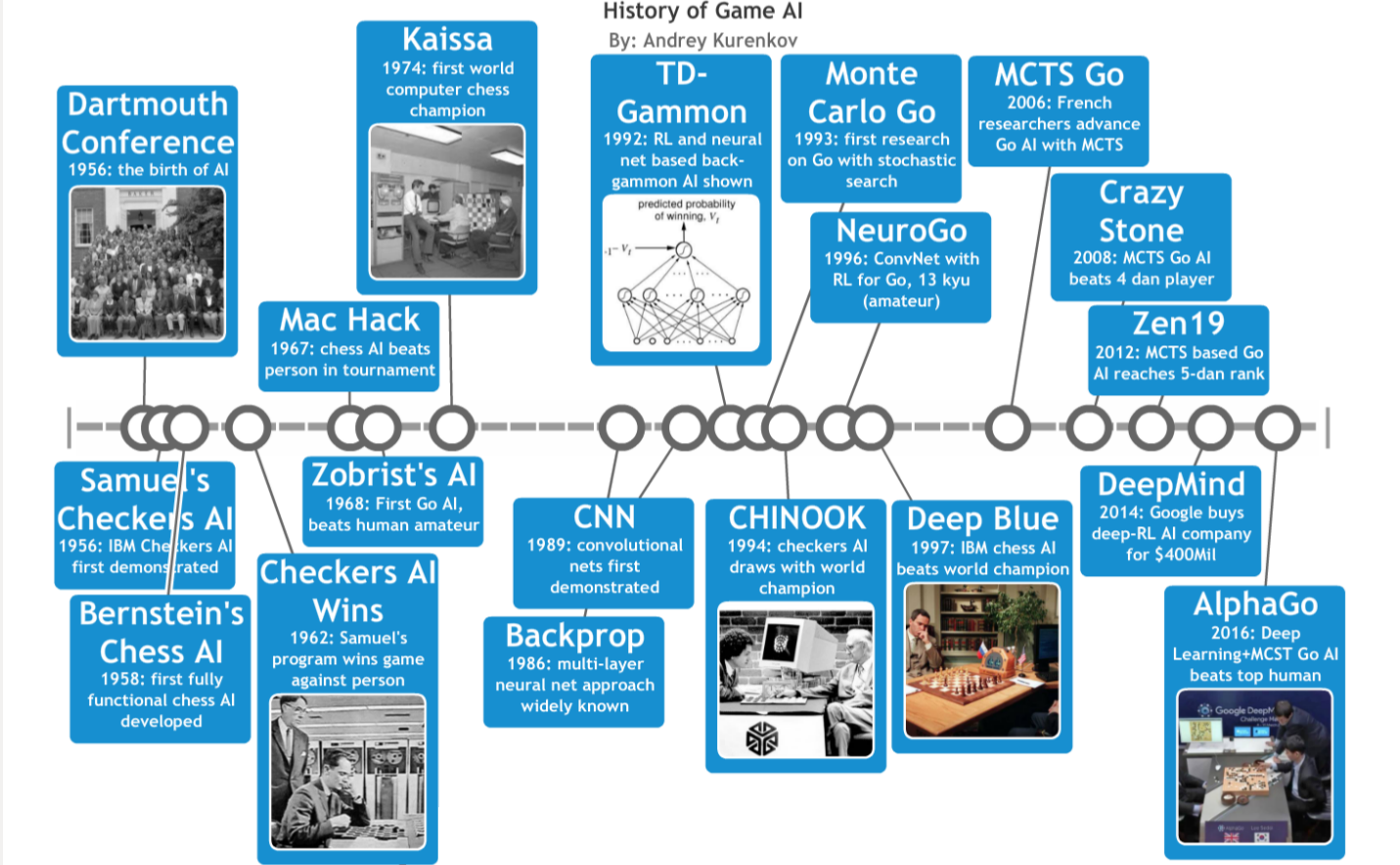
关于游戏智能的一系列论文的时间轴
序言:最终,围棋游戏里算法胜过了人类
2016
2016年03月09号,谷歌设计的程序 AlphaGo 击败了世界级的卫冕冠军李世乭,这让 AI 达到了历史性的里程碑。围棋是像象棋这样的双人对战棋盘游戏,但是更多的移动可能性和评估难度让围棋成为 AI 领域内的难啃的硬骨头。所以当 AlphaGo 一周四场比赛以三比一的战绩战胜李世乭后,这成为一起震动世界的历史性事件。怎样大的事件?媒体如此精确的描述 AlphaGo:“人工智能的重大突破”,它达到了“人工智能研究领域最受欢迎的里程碑之一”的评价。评论委员会不那么保守,许多人认为AlphaGo的胜利是可怕的甚至是超人类智能(superhuman AI)即将出现的迹象。
数月前的一天,在 Google 首次宣布开发之后1,我兴奋地浏览了AlphaGo 的这篇论文。这让我觉得这是一个在围棋领域令人印象深刻的飞跃,通过已经成功的技术的完美结合来实现。所以,当媒体对AlphaGo的狂热爆发时,我想写一个小贴子,解释为什么从AI的角度来说很酷,但同时解释为什么它不是可怕的天网AI的幼儿版(译注:终结者中的天网)。在这样做的过程中,我在60年的游戏AI历史中偶然发现了许多值得关注的发展和细节,我无法停下来写这篇短小的博客文章。所以,我希望你们喜欢这个对AlphaGo之前的所有令人激动的想法和历史性里程碑的简要总结,并引发这个最新的人类智慧奇迹。
声明:我不是相关专家,更深入的研究和勘误:
职业作家 Alan Levinovitz 写的围棋的神奇——计算机仍无法战胜的古老游戏
谦逊的开始
1949
自从现代计算机诞生以来,人们开始思考它是否可以匹配或取代人类智能。而且由于测量人类智能是困难的,许多人推断他们可以通过首先使计算机擅长某些挑战人类智力的任务来解决这个问题。所以,策略游戏。早在1949年,克劳德·香农(Claude Shannon)就发表了关于如何使用计算机来玩国际象棋这个话题的想法2。他既证明了解决这个问题的有效性,又确定了其范围:
“国际象棋机器是一个理想的开始,因为:(1)在允许的操作(动作)和最终目标(将死)中,问题是明确的; (2)既不是那么简单的微不足道,也不是太难去找到满意的解决方案; (3)国际象棋通常被认为是需要“思考”才能玩的; 解决这个问题将迫使我们要么承认机械化思维的可能性,要么进一步限制我们的“思考”概念; (4)国际象棋的离散结构很好地融入了现代计算机的数字本质。 …显而易见,问题不在于设计一台机器来完美的玩国际象棋(这是非常不切实际的),也不是一个只玩合法国际象棋(这是微不足道的)。 我们想玩一个熟练的游戏,或许可以和一个好的人类玩家相提并论。”
香农的提出的方法今天被称为Minimax(以约翰·冯·诺伊曼(John Vonn Neuman)的极大极小值定理命名,1928年他证明了这一点),它对未来游戏智能将会产生巨大的影响。这或许是实现游戏智能的最明显的方法。 这个想法是假设两个玩家都会考虑整个游戏的所有未来动作,所以玩的最佳。 换句话说,你总是应该选择一个动作,即使对手选择了这个动作以及你的未来的每一个动作的绝对最佳回应,在比赛结束时你仍然可以获得最高分。
用计算机很容易能做到这点。通过表示位置(或状态)和游戏规则,所有需要做的就是编写一个程序,从当前状态中生成所有可能的下一个游戏状态,以及这些状态的可能状态,等等。 通过这样做,程序可以模拟游戏超过当前点,并在游戏结束时建立可能的路径树。 然后,它只需要按照最佳路径的动作来达到最佳游戏结局。 这样做的缺点是没有把握对手可能犯下的错误,但总的来说是一个非常安全和明智的策略。
附:极大极小值定理的步骤:
分解极大极小值的工作步骤:
- 在你要移动棋子的时候,考虑一下你可以采取的所有可能的举措;
- 对于你每一个可能的移动,考虑对手所有可能的回应移动;
- 现在考虑对手回应的每一种可能操作,并不断思考后面的步骤直到游戏结束时(你会得到一个分数);
- 假设和你一样,对手可以在整个游戏结束时考虑所有的移动,所以决不会犯错误 - 他们将会发挥最佳效果,并且假设你将发挥最佳效果。 选择目前的行动来最大化你的最终得分,假设你的对手将总是选择所有未来的举动,以最大限度地减少你的分数,以回应你做出的任何移动。
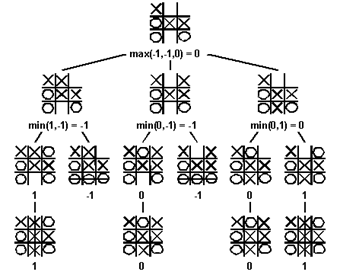
在简单的Tic-Tac-Toe游戏中的例子minimax游戏树。树中的每一个连续层代表可能的游戏状态,在当前游戏状态之前有一些移动,传统上被称为一层(ply)。
还有一个细节:虽然在理论上Minimax搜索涉及到所有路径到游戏结束,实际上这是不可能的,因为跟踪每一个模拟未来的额外移动会导致游戏状态的组合爆炸。也就是说,每一步都有一些选项(被称为分支因子(branching factor)),所以树中的每一个附加层(ply)大致乘以该分支因子的大小。如果分支因子是10,那么前进一步将需要考虑10个游戏状态,两个前进要求10 + 10 * 10 = 110,三个移动到达1110,等等。所以,我们使用评价函数来评估游戏尚未结束的位置。评价函数可以简单地计算每个玩家的棋子数量,也可以更加复杂,使得可以仅仅搜索前面3或6个棋子(或者3或6个棋子的深度)而不是涉及一般国际象棋游戏40个棋子的动作。
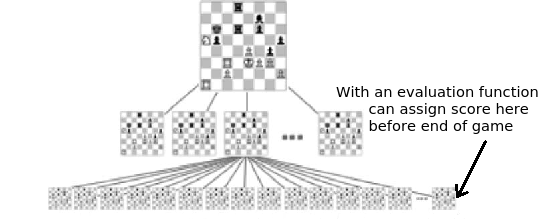
在搜索树中评估游戏中的位置
香农的论文中定义了如何使用 Minimax 和评价函数,并为将来在国际象棋AI上的工作设定了路线,提出了两种可能的策略:(A)用评价函数进行强力Minimax树搜索,或者(B)使用“似是而非的移动生成器”,而不是仅仅依靠游戏规则来查看树搜索过程中每层的一小部分的下一步移动。国际象棋比赛常常根据他们主要基于哪种策略而被分类为“A型”或“B型”。香农特别指出,第一个策略是简单的,但不实际,因为随着每一个额外的层数和可能的位置(状态空间)总数的巨大,状态的数量呈指数增长。对于第二种策略,香农从国际象棋棋手那里获得灵感,他们选择性地只考虑有前途的棋步。然而,一个好的“似是而非的移动生成器”并不是那么好写的,所以在策略(A)中的大规模搜索仍然是有用的。 我们将在后面看到,深蓝(击败国际象棋世界冠军加里·卡斯帕罗夫的节目)基本上是两种方法的结合。

香农展示了他制作的一台机器,试图制作限制版国际象棋的编程规则。
1951
但是,支持“深蓝”的超级计算机距离出生还有几十年时间,这对50年代早期计算机先驱者来说最多是个梦想(事实上,着名的摩尔定律直到十年之后才有定义)。事实上,第一个国际象棋程序不是用硅或真空管,也不是用任何数字计算机,而是用人类大脑的粘稠的肉质神经元 - 阿伦·图灵的神经元来精确地运行。数学家兼开创性的AI思想家图灵(Turing)花费了数年时间研究他在1951年完成的国际象棋算法,并称之为TurboChamp。3
TurboChamp并不像香农提出的系统那样广泛,而且在未来的标准中非常基础,但是它仍然可以发挥国际象棋的作用。 在1952年,图灵手动执行了算法,那一定是一个极其缓慢的游戏,程序最终失败了。 图灵还在国际象棋AI上发表了自己的想法,并认为原则上可以从经验中学习和在人类层面上进行游戏的程序是完全可能的4。 就在几年之后,第一个电脑国际象棋程序将被执行…
理论变成了代码
1956
所有这些都发生在 AI(人工智能领域)之前。这可以说是发生在1956年的达特茅斯会议上,这是一个为期一个月的关乎未来 AI 的头脑风暴会议,也是在这个会议上诞生了“人工智能”这个词(或者参见维基百科)。除了大学的数学家和研究人员(其中包括克劳德·香农)外,还有两名IBM工程师:Nathaniel Rochester 和 Arthur Samuel。Nathaniel Rochester 领导的一个小组开创了在实现人工智能领域的突破的IBM人的传统,Arthur Samuel 是其小组的第一位成员。
自1949年依赖,Samuel 一直在思考机器学习(算法使计算机能够通过学习而不是通过人工编码的人类解决方案来解决问题),并特别专注于开发能够学习跳棋游戏的人工智能。跳棋有1020个可能的棋盘位置,比国际象棋(1047)或者围棋(10250,稍后还会讨论……)要简单的多,但仍然复杂到难以掌握。考虑到那时缓慢而笨重的计算机,跳棋是很好的第一个目标。Samuel利用他在IBM所拥有的资源,尤其是他们的第一台商用计算机(IBM 701),开发了一个可以很好地发挥跳棋游戏的程序,这是第一个在计算机上运行的AI游戏。他在“跳棋游戏中使用机器学习的一些研究”中总结了他的成就5:
“在跳棋游戏中已经对两个机器学习程序进行了一些详细的调研。已经做了足够的工作来验证这样一个事实,即一台计算机可以被编程,以便它能学习比编写该程序的人玩更好的棋子游戏。此外,当仅给出游戏规则,一些方向感,和与游戏有关的一些冗余的和不完整的参数列表后,它能在非常短的时间内(8或10小时的机器对弈时间)学习到如何下棋,但其正确的标志和相对权重是未知的,没有说明的。这些实验验机的机器学习原理当然也适用于许多其他情况。”
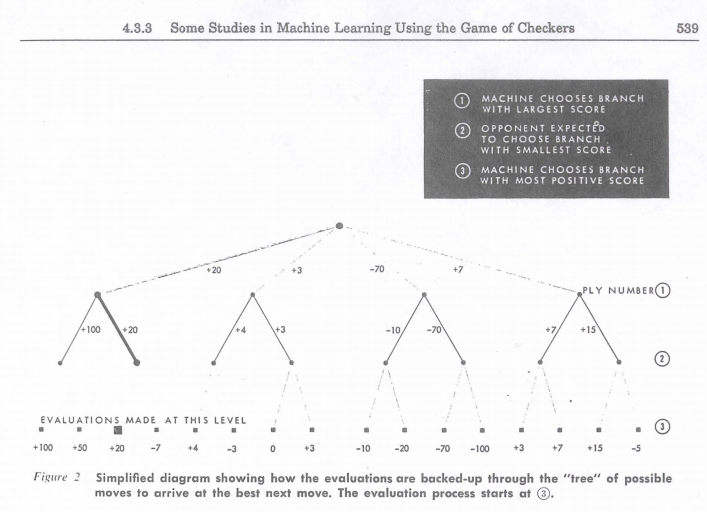
Samuel的论文里用来解释Minnimax的图示
从根本上讲,该方案是基于Minimax,但还有一个非常重要的方面:学习。随着时间的推移,程序变得越来越好,没有人为干预,通过两种新颖的方法:(A)“死记硬背” - 意味着它可以存储以前用Minimax评估过的特定位置的值,所以不需要花费计算资源考虑移动 (B)“通过一般化学习”,即根据程序所记录的以前的对弈过程,修改不同参数的乘数(从而修改评价函数)。 乘数会被改变以降低给定棋盘位置的计算好处(根据评价函数)和其实际好处(游戏完成后的统计计算)的差异。
死记硬背的学习方式在一段时间内使得程序明显的更有效率和能力,它运作良好。但却是一般化的学习方法(learning-by-generalization)带来了具有开拓性的创举,因为它表明,程序可以“直观地”知道一个游戏的位置是多么好,而没有大量的未来动作模拟。不仅如此,这个程序还会通过自己过去版本的对弈来学习,这成为了后来的AlphaGo的关键组件!但我们还是别太超前了……
附:Samuel学习程序的引用
以下是有关每种学习策略优点的文章的有趣摘录:
“一些有趣的比较可以在通过一般化学习程序所开发的游戏风格与早期的死记硬背程序所开发的风格之间进行。死记硬背的程序很快就学会了在开场动作中模仿大师的动作。中场比赛总是很差,但是很容易学会如何在比赛结束时避开大部分明显的陷阱,并且通常可以在稍微有利的情况下赢下比赛。一般化学习程序从未学会常规比赛礼仪,而且它的开放势头很弱。另一方面,它很快就学会了打出好的中场比赛,并能再短时间内击败对手。
显然,在任何具体行动的结果被拖延的情况下,或者在那些需要高度专业化的技术的情况下,死记硬背学习程序是最有帮助的。与此相反,一般化学习程序对于可用排列数量多的条件且任何具体行动的后果不延迟的情况是最有帮助的。”

Samuel论文中另一个死记硬背学习的图示
这些想法不仅是开创性的,而且还在实践中发挥作用:该程序可以发挥跳棋的可观的游戏,鉴于当时有限的计算能力,这是不小的壮举。 因此,作为这个伟大的回顾性的细节,当Samuel的计划在人工智能的早期阶段(事实上在达特茅斯会议的同一年)首次被证明时,它给人留下了深刻的印象:
“Samuel没有花多长时间就做出了一个程序,它能玩出一场可观的跳棋比赛,并能轻易击败跳棋新手。1956年2月24日在电视上首次公开表演。IBM总裁Thomas Watson安排该项目向股东展示。他预测这会导致IBM股票价格上涨十五点。它做到了。”

“1956年2月24日,阿瑟·塞缪尔的“跳棋”节目在IBM 701上播放,在电视上向公众展示。”
1957
但是,这是跳棋 - 而大家真正关心的是国际象棋?那么,IBM的员工又是谁开创了第一个国际象棋AI,和Samuel一样,那些员工是由Nathaniel Rochester监督的。这项工作主要由数学家和经验丰富的国际象棋棋手亚历克斯·伯恩斯坦(Alex Bernstein)领导。和塞缪尔一样,他决定从个人利益出发来探索这个问题,并最终领导在1957年完成的IBM 701上实现功能齐全的国际象棋6。这个程序也使用了 Minimax,但缺少了任何学习能力并最多只能预测4步,每步只能考虑7个选项。 直到七十年代,大多数国际象棋游戏节目也会受到类似的限制,再加上一些额外的逻辑来选择哪种动作来模拟,就像1949年香农所描述的类型(B)策略。伯恩斯坦的方案有一些启发式的(便宜的计算“经验法则”)来选择最好的7个动作来模拟,这本身就是一个新的贡献。 不过,这些限制意味着该方案只能实现非常基本的国际象棋游戏。
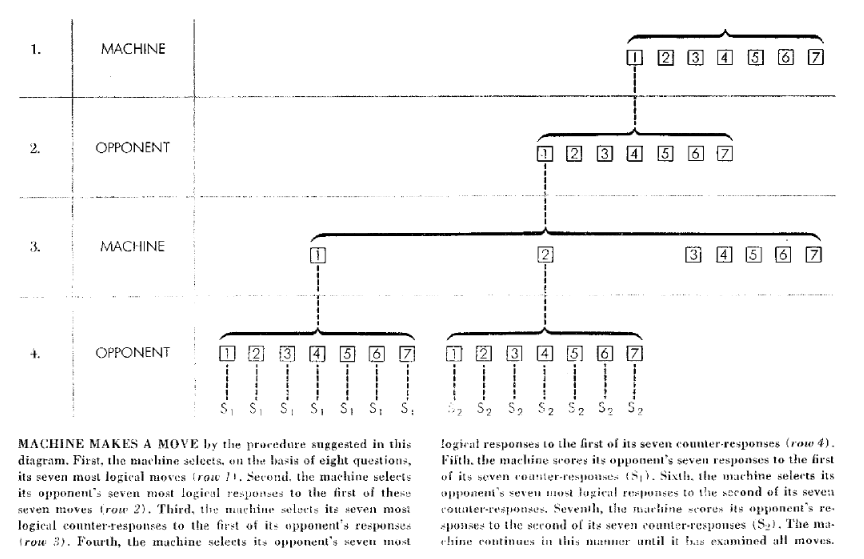
从有关它的文章中可以看出伯恩斯坦计划所做的有限的极大极小值搜索

Bernstein 在和他的程序对弈
Bernstein的象棋程序在电视报道成为焦点
尽管如此,这是第一个功能齐全的国际象棋的游戏程序,并证明即使极其有限的Minimax搜索与一个简单的评价函数且没有学习功能,也可以战胜国际象棋的新手们。这可是在1957年!在接下来的几十年里将会发生那么那么多……
致谢
多谢Abi See,Pavel Komarov,和Stefeno Fenu 的帮助,我才能完成这篇文章。
原文:
http://www.andreykurenkov.com/writing/a-brief-history-of-game-ai/
参考:
-
David Silver, Aja Huang, Christopher J. Maddison, Arthur Guez, Laurent Sifre, George van den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, Sander Dieleman, Dominik Grewe, John Nham, Nal Kalchbrenner, Ilya Sutskever, Timothy Lillicrap, Madeleine Leach, Koray Kavukcuoglu, Thore Graepel & Demis Hassabis (2016). Mastering the game of Go with deep neural networks and tree search. Nature, 529, 484-503. ↩
-
Shannon, C. E. (1988). Programming a computer for playing chess (pp. 2-13). Springer New York. ↩
-
A Jenery (2008). A Short History of Computer Chess. chess.com link ↩
-
Alan Turing (1953). Chess. part of the collection Digital Computers Applied to Games. in Bertram Vivian Bowden (editor), Faster Than Thought, a symposium on digital computing machines, reprinted 1988 in Computer Chess Compendium ↩
-
Samuel, A. L. (1959). Some studies in machine learning using the game of checkers. IBM Journal of research and development, 3(3), 210-229. ↩
-
Bernstein, A., & Roberts, M. D. V. (1958). Computer v chess-player. Scientific American, 198(6), 96-105. ↩